IPMSM "D1モデル" 解析結果¶
以下に [CITE2013] により公開されている結果と,[paper2015] で紹介された解析結果をまとめます。
測定には1研究機関,解析には計7研究機関が参加しており,各研究機関の所有するプログラムにより解析を行ったものです。
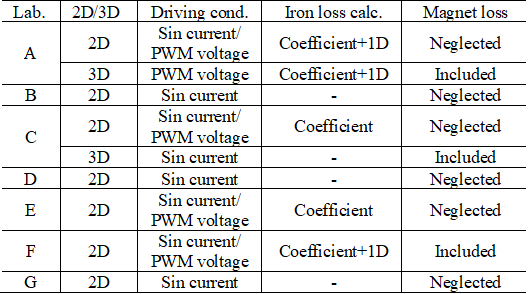
図 40 D1model 研究機関と計算手法 (出典:[CITE2013])¶
測定条件¶
測定で用いたモータ制御ブロック図と,測定条件を示します。
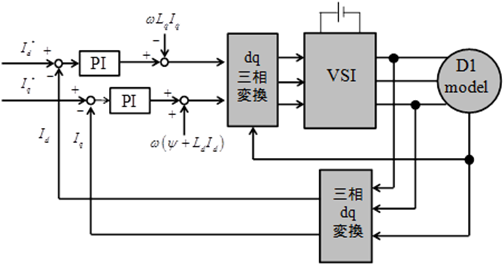
図 41 モータ制御ブロック図 (出典:[CITE2013])¶
電流 [Arms] |
4.4 |
電流進角 [deg] |
20 |
回転数 [min-1] |
1500 |
インバータ直流電圧 [V] |
200 |
キャリア周波数 [kHz] |
10 |
測定装置¶
試験装置概要図と測定装置仕様を示します。供試モータには固定子に熱電対を3箇所備え付け,銅損測定のための温度測定を行ったものです。
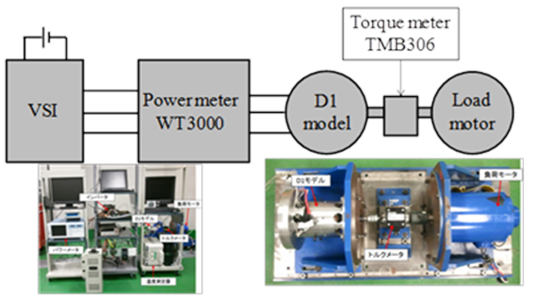
図 42 試験装置概要 (出典:[CITE2013])¶
測定装置の仕様はDmodelと同じです。
損失測定結果¶
技術報告 [CITE2012] において,損失測定について検討が行われているので紹介します。磁界解析より鉄損を算出することができますが,測定結果と比較する際の参考になると思われるため紹介します。
鉄損測定に際しては,巻線抵抗の温度依存性と機械損失の温度依存性,ならびにエンコーダの位置ずれに着目して測定を行ったものです。鉄損の算出は次式により行います。
ここで,\(P_{input}\) はパワーメータにより測定されるインバータの出力パワー,\(P_{output}\) はトルクメータの出力トルク平均値とモータ角速度の積として求めるモータ出力パワー,\(W_{copper}\) は温度依存性を考慮した抵抗と電流実効値により算出する銅損,\(W_{mechanical}\) はベアリングに代表される機械損失です。 図 D1model 巻線抵抗温度依存性 (出典:[CITE2013]) に巻線抵抗の温度依存性を示します。パワーメータの出力端子からの抵抗値(巻線抵抗+配線抵抗)を測定対象とし,W-U線間に直流を通電し,測定した電圧,電流からインピーダンス法を用いて温度特性を取得しました。モータ駆動時には各相のコイル温度の平均値から図 D1model 巻線抵抗温度依存性 (出典:[CITE2013]) を用いて抵抗値を算出し,銅損を算出しています。 機械損失の測定結果を表 暖気および電流通電による機械損差異 (出典:[CITE2013]) に示します。永久磁石を取り出した回転子を用いて負荷モータにて一定回転し,回転直後および1時間後の機械損を測定した結果です。また,ステータに電流を通電して温度上昇させたのち測定した機械損も示します。温度上昇による機械損失の低下が示されており,測定鉄損がおおよそ5Wに対し2Wもの差が出ることが確認されています。 表 位置合わせ方法による出力差異 (出典:[CITE2013]) にはエンコーダの位置合わせ方法の差異によるモータ出力パワーの差異を測定した結果を示します。ここで,\(\beta\) =90degはd軸電流のみを通電して出力トルクが0になるように位置を調整する方法,Back-EMFは無負荷誘起電圧のゼロクロスを用いて位置を合わせる方法,DCは一相に直流電流を通電し,ロータが磁気的にロックする位置を0degと設定する方法です。位置合わせの方法によっても出力パワーが2W程度変化することが確認されています。 以上の結果を用いて測定した各鉄損測定値を表 損失測定値(位置合わせ方法による差異)(出典:[CITE2013]) に示します。機械損失は定格電流通電時の値を用い,各位置合わせの方法にて測定した結果です。測定鉄損は4.5Wから5.4Wの値となり,測定手法により約20%のばらつきをもつことが確認されました。
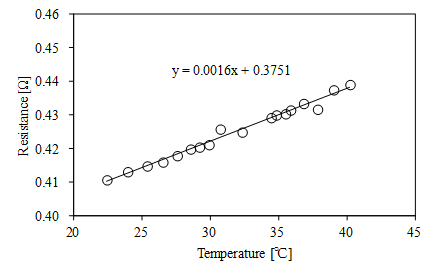
図 43 D1model 巻線抵抗温度依存性 (出典:[CITE2013])¶
No load |
No load |
Load |
Load |
|
|---|---|---|---|---|
Start |
End |
Start |
End |
|
Torque [mNm] |
41 |
37 |
30 |
28 |
Mechanical loss [W] |
6.5 |
5.8 |
4.7 |
4.4 |
\(\beta\) =90deg |
Back-EMF |
DC |
|
|---|---|---|---|
Phase [deg] (\(\beta\) =90deg standard) |
--- |
+0.88 |
+7.55 |
Torque [Nm] |
1.775 |
1.775 |
1.761 |
Output power [W] |
278.8 |
278.8 |
276.7 |
\(\beta\) =90deg |
Back-EMF |
DC |
|
|---|---|---|---|
Iron loss [W] |
4.53 |
5.44 |
5.05 |
Copper loss [W] |
25.36 |
25.18 |
25.32 |
Mechanical loss [W] |
4.4 |
4.4 |
4.4 |
Total loss [W] |
34.3 |
35.0 |
34.8 |
Output power [W] |
276.7 |
278.8 |
278.8 |
Input power [W] |
313.11 |
313.84 |
313.44 |
Efficiency [%] |
90.46 |
90.24 |
90.25 |
解析メッシュ図(例)¶
技術報告 [CITE2013] では,各研究機関で異なるメッシュを使用して解析を行ったものです。ここでは例として研究機関Aのメッシュ図を示します。
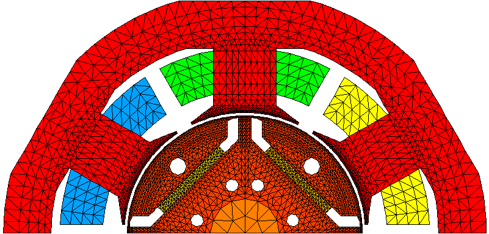
図 44 D1model 2Dメッシュ図 (出典:[paper2013])¶
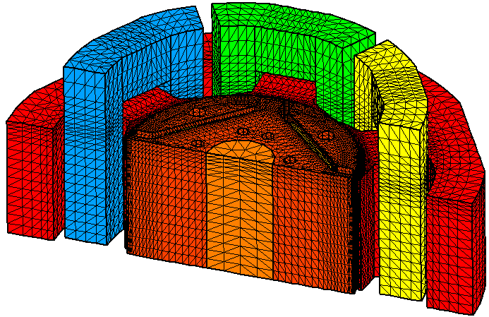
図 45 D1model 3Dメッシュ図 (出典:[paper2013])¶
無負荷誘起電圧¶
無負荷時の結果として,無負荷誘起電圧( \(1500 min^{-1}\) )の結果を,測定波形と比較したものを示します。
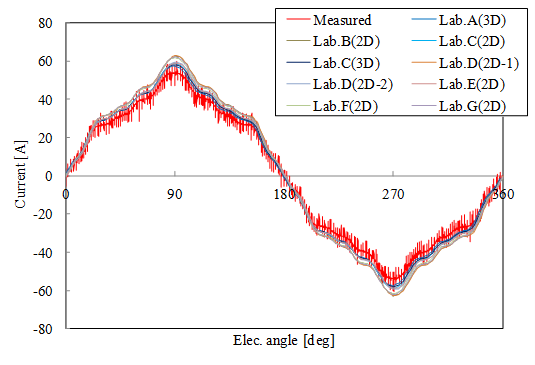
図 46 D1model 線間誘起電圧波形の比較 (出典:[paper2013])¶
無負荷線間誘起電圧測定結果
D1model_back_emf.csvのダウンロード
技術報告に記載はありませんが,参考までに研究機関Cの相誘起電圧の成分を測定結果と比較して示します。
また,誘起電圧の1次成分より算出したd軸磁石磁束も示します。誘起電圧の一次成分からd軸磁石磁束を算出するために次式を使用しています。ここで,1500は回転数です。
コイル鎖交磁束をdq変換したd軸成分からも算出しています。
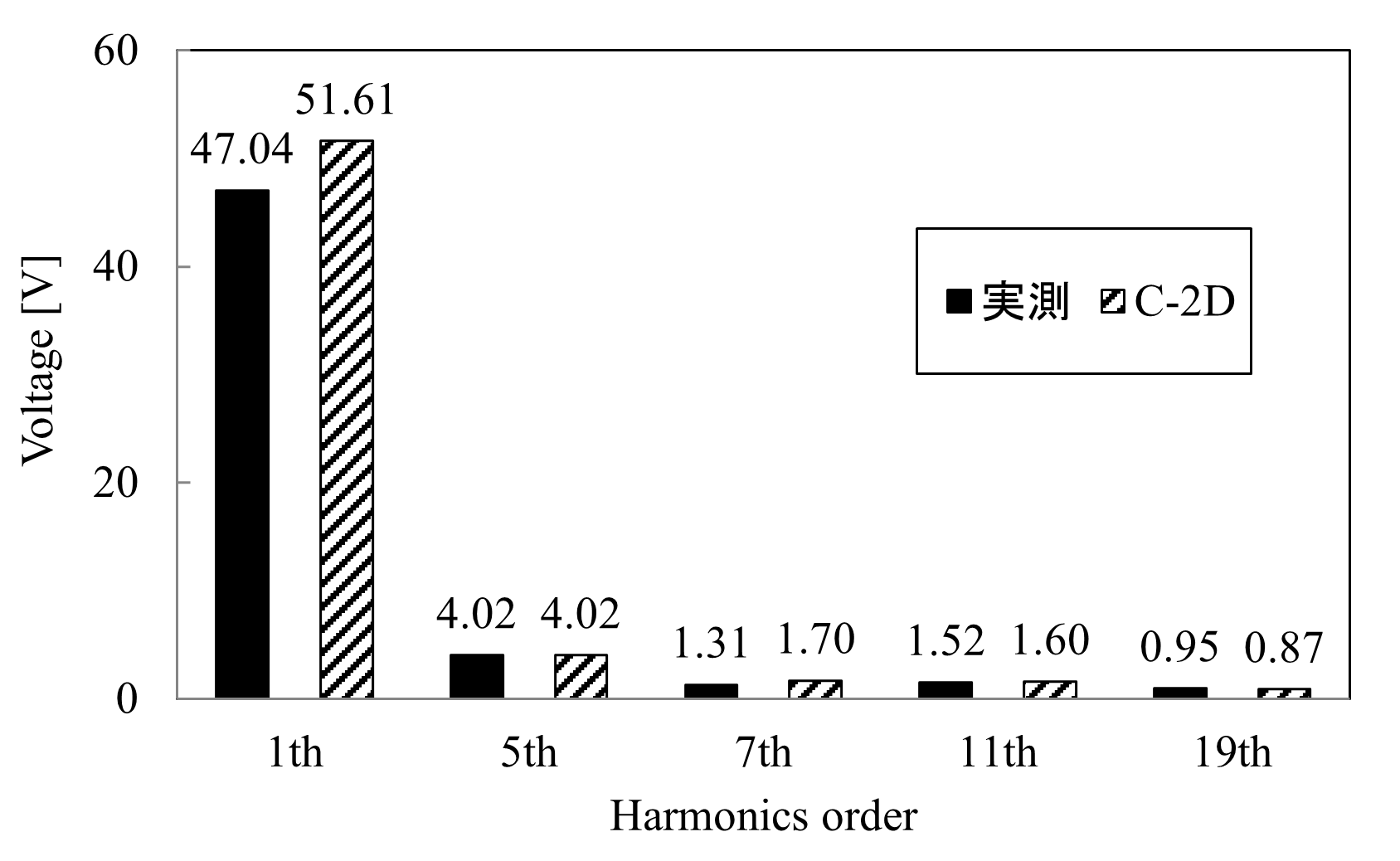
図 47 D1model 相誘起電圧FFT結果の比較¶
次数 |
測定 |
解析 |
|---|---|---|
1 |
47.038 |
51.608 |
5 |
4.017 |
4.016 |
7 |
1.305 |
1.700 |
11 |
1.516 |
1.597 |
19 |
0.950 |
0.866 |
\(\psi_m\) (mWb) |
|
|---|---|
測定 |
105.9 |
解析(電圧の1次成分より) |
116.2 |
解析(コイル鎖交磁束のd軸成分) |
116.2 |
(参考)コギングトルク¶
技術報告に記載はありませんが,参考までに研究機関Cのコギングトルク波形を示します。peak-to-peakは二次元解析(2D)で0.079, 三次元解析(3D)で0.072です。
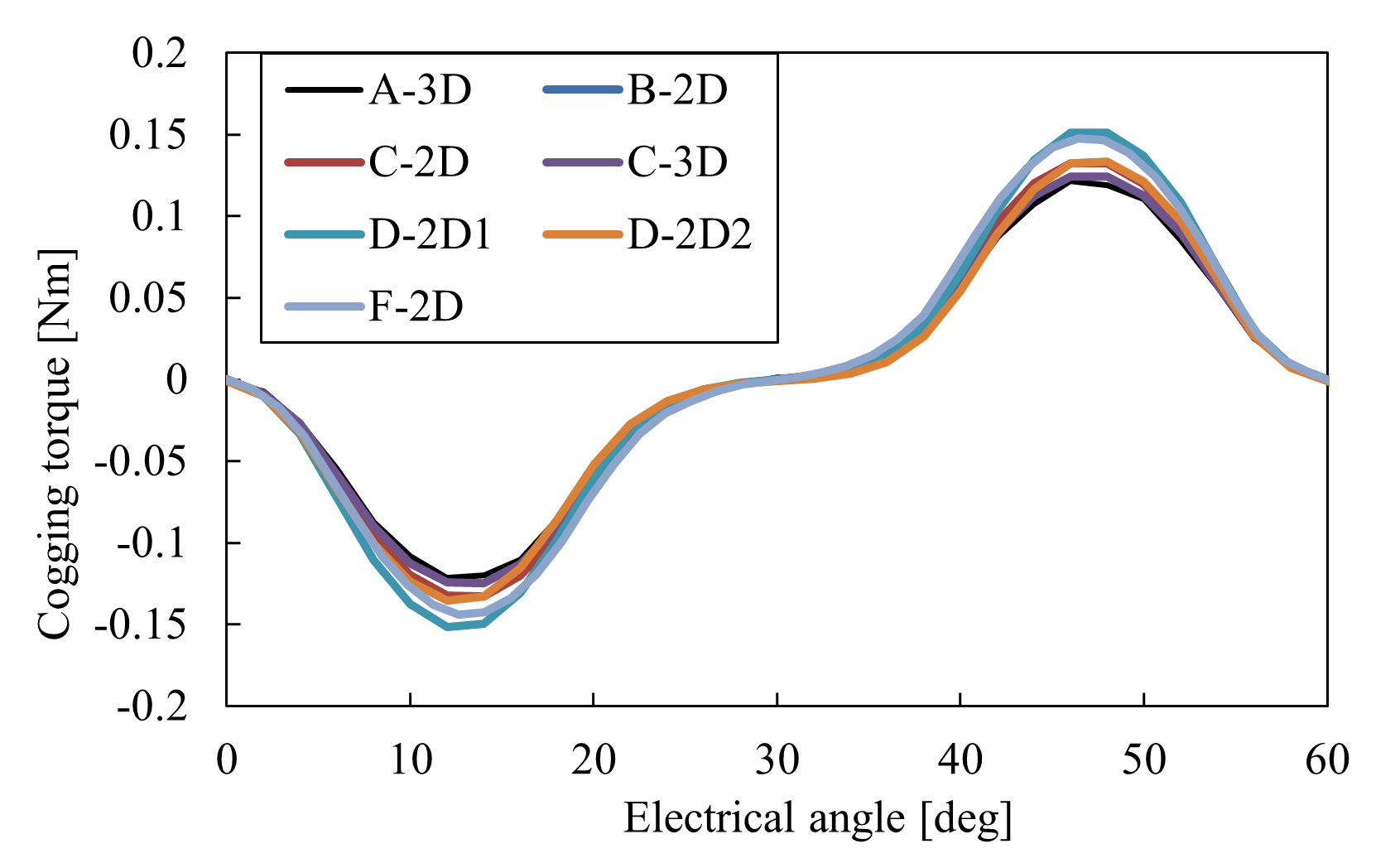
図 48 D1model コギングトルク波形¶
2D解析 |
3D解析 |
|
|---|---|---|
peak-to-peak (Nm) |
0.266 |
0.250 |
インダクタンス特性¶
dq軸インダクタンス特性を示します。IPMSMではd軸インダクタンスLdとq軸インダクタンスLqの差(Lq- Ld)によるリラクタンストルクを発生できるため,基本的にマグネットトルクのみである表面磁石構造のPMSMよりも平均トルクを大きくすることができます。
インダクタンスは測定,解析共にid, iq単独通電によりLd , Lqを分離して算出しています。
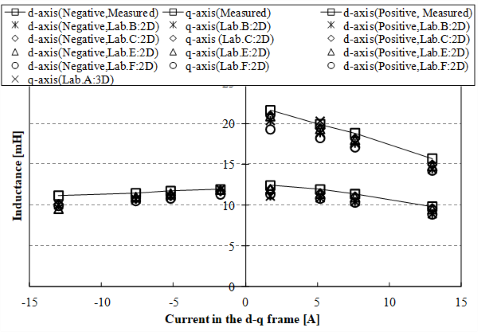
図 49 D1model インダクタンス特性 (出典:[paper2013])¶
トルク特性¶
定格条件(仕様値トルク1.8Nm)でのトルク―電流進角特性(4.4Arms)とトルクー電流特性(電流進角0deg)を示します。解析結果は算出したLd , Lqと \(\psi_m\) を用いてトルクを算出した結果です。なお,二次元解析結果です。トルク―電流進角特性では電流進角0deg時に測定結果(Measured)と解析結果(FEA)10.9%程の差がありますが,電流進角に対しておおよそ傾向は一致しています。トルクー電流特性では,測定結果(Measured)は電流が高くなるにつれてトルクがやや小さくなる傾向があります。Theoryは,\(T_m = N_p \times \psi_m \times I_q\) より算出したマグネットトルクです( \(N_p\) は極対数)。先に示したように測定結果と解析結果のd軸磁石磁束 \(\psi_m\) はやや差がありますが,それ以上に電流が大きくなるにつれ測定と2D解析の差異が大きくなっています。3D解析では測定結果に近い値が得られています。
トルク波形は研究機関Aによる結果で,平均トルクは各研究機関と測定結果を比較したものです。平均トルクはおおよそ解析結果の方が測定結果よりも9%ほど大きいです。
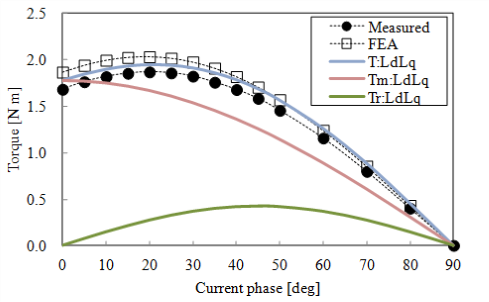
図 50 D1model トルク―電流進角特性(3Arms) (出典:[paper2013])¶
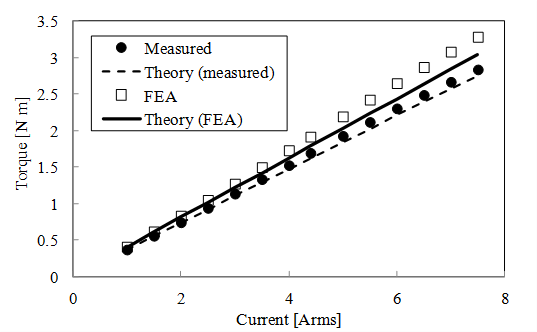
図 51 D1model トルク―電流特性(電流進角0deg) (出典:[paper2013])¶
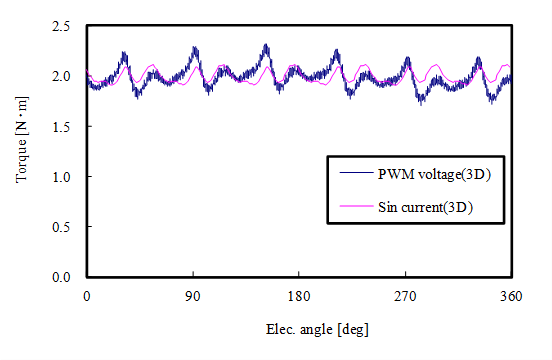
図 52 D1model トルク波形 (出典:[CITE2013])¶
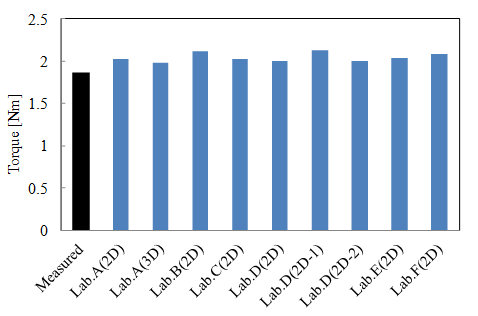
図 53 D1model 平均トルク (出典:[paper2013])¶
PWM印加時の結果¶
定格条件での測定結果として,電圧と電流波形を示します。
インバータ直流電圧 [V] |
200 |
キャリア周波数 [kHz] |
5 |
回転数 [min-1] (鉄損特性) |
1500 |
電流振幅 [Arms] |
4.4 |
電流進角 [deg] |
20 |
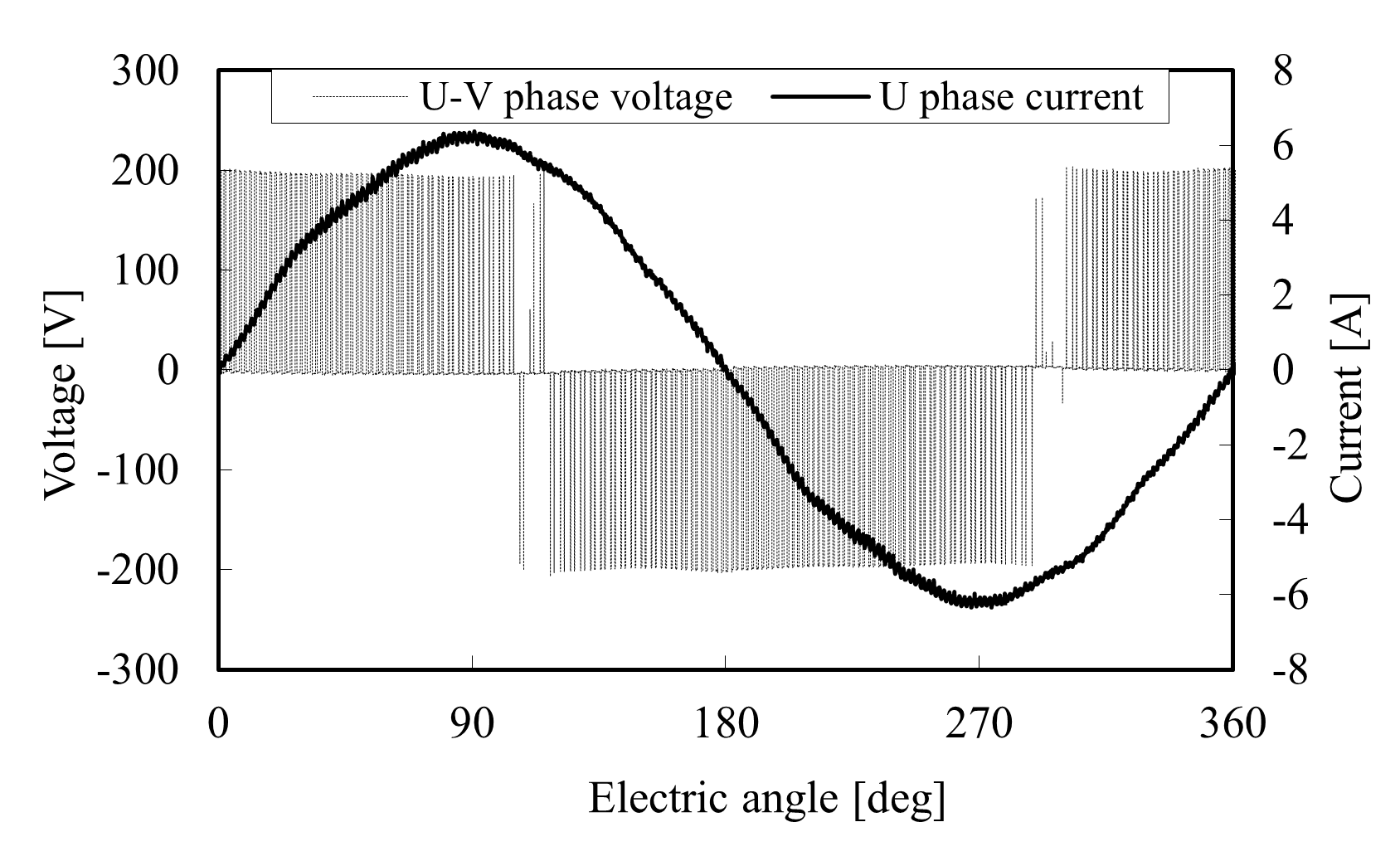
図 54 D1model 相電流,線間電圧波形(測定値) (出典:[paper2015] )¶
相電流,線間電圧波形(測定値)
D1model_pwm_vi.csvのダウンロード
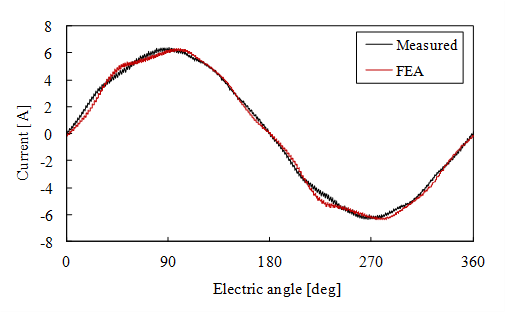
図 55 D1model 相電流波形の測定結果・解析結果の比較 (出典:[paper2015] )¶
鉄損特性¶
解析での鉄損算出には各要素の磁束密度波形を用いて後処理にて算出する方法が簡便で精度よく算出できることが実証されています。 加えて,電磁鋼板中の渦電流損の周波数依存性を考慮するために,後処理一次源渦電流解析が併用されています。
測定は \(1500 min^{-1}\) のみで測定され,入力から出力(トルク),機械損(ベアリングの摩擦損),電機子巻線の銅損を差し引いた残りを鉄損として算出しています。鉄損の測定値は,5.437Wです。
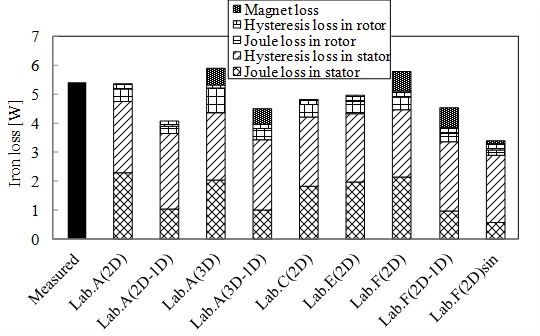
図 56 D1model 鉄損特性 (出典:[paper2013])¶
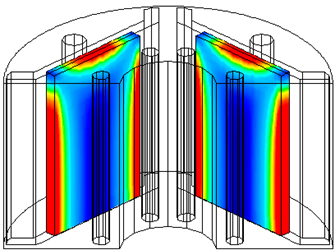
図 57 D1model 永久磁石の渦電流密度分布および損失密度分布 (出典:[paper2013])¶
マグネットトルクが理論値を上回る理由¶
技術報告 [CITE2013] では,電流進角0degにおいて,マグネットトルクが理論値を上回る理由について考察されています。ここでは,その一部を紹介します。
D1モデルの電流進角β=0degで,トルクが理論値であるマグネットトルクよりもFEA計算値,測定値共に大きくなる要因を,d軸磁束に着目した検討が行われました。集中巻の場合に現れる現象です。
MSMの特性をdq軸で考える場合,磁束とインダクタンスの関係は,次式で表されます。
ここで,\(\psi_{0d}\) , \(\psi_{0q}\) はdq軸のコイル鎖交磁束,\(\psi_d\) , \(\psi_q\) はコイル鎖交磁束,\(L_d\) , \(L_q\) はdq軸インダクタンス,\(L_{dq}\) , \(L_{qd}\) はdq軸相互インダクタンス,\(\psi_m\) はd軸磁石磁束です。
一般的に,測定と解析ではインダクタンスマトリックスの非対角成分はゼロ,すなわちdq軸間が独立である(磁束の干渉がない)として,トルク \(T_m\) を次式で表されます。
ここで,\(P_n\) は極対数です。 第2式は,磁束を永久磁石に起因するものと電流に起因するものに分けていることになります。 電流進角 \(\beta = 0 deg\) でのトルクは \(i_d = 0\) であるため,第2式では右辺第1項の磁石磁束の項のみとなり,一般的に理論値のマグネットトルクと言われます( \(T = P_n \psi_m i_q\))。そのため,もしdq軸の磁束の干渉がある場合,第2式によるトルク算出では不十分であることがわかります。一方,第1式はdq軸間干渉分も含んだ表現であるため,常に成り立つと考えられます。
図 トルク―電流実効値特性(D1モデル) (出典:[CITE2013] ) に,電流進角0degでのトルクを,FEA結果(FEA)と,FEA結果の各電流実効値でのd軸磁束 \(\psi_{0d}\) を使用した場合( \(\psi_{0d} i_q\))の結果を,理論値(Theory)と比較して示します。ここで,磁石磁束 \(\psi_m\) は無負荷時のd軸磁束です。これは,dq軸が独立であるとした場合の比較です。これより,FEA結果と各電流実効値でのd軸磁束を使用した場合は非常に良く一致していることが確認できます。参考までに,図 トルク―電流実効値特性(Dモデル) (出典:[CITE2013] ) にDモデルでの結果を示します。Dモデルでは,理論値とFEA結果,各電流実効値でのd軸磁束を使用した場合すべて非常に良く一致しています。図 d軸磁束 \psi_{0d} と磁石磁束 \psi_m の差分 (出典:[CITE2013] ) に各電流実効値のd軸磁束と無負荷時より算出した磁石磁束の差分を示します。これらより,Dモデルでは電流によらず磁石磁束はほぼ一定値(磁束の差分が小さい)であるのに対し,D1モデルでは電流が大きくなるにつれd軸磁束の差分も大きくなっています。つまり,dq軸が独立していると考えた場合,電流進角?=0degでは理論的にはq軸の磁束のみが発生するはずであるが,D1モデルではd軸にも流れ込んでおり,それがトルクに寄与しているためだと考えられます。図 トルク―電流実効値特性(Dモデル) (出典:[CITE2013] ) に示すD1モデルの電流値ごとの磁束分布を見ると,電流値によって磁束の流れが変わっていることからも推察できます。
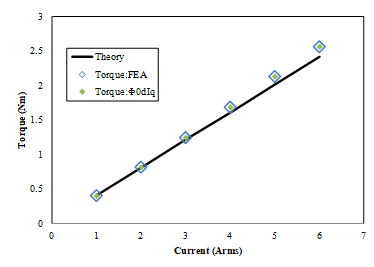
図 58 トルク―電流実効値特性(D1モデル) (出典:[CITE2013] )¶
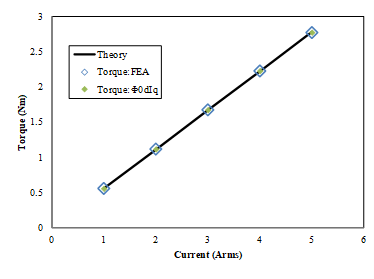
図 59 トルク―電流実効値特性(Dモデル) (出典:[CITE2013] )¶
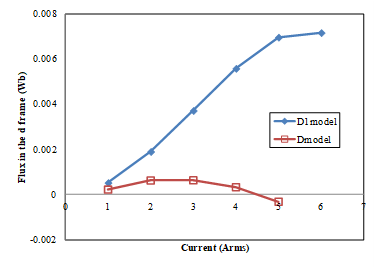
図 60 d軸磁束 \(\psi_{0d}\) と磁石磁束 \(\psi_m\) の差分 (出典:[CITE2013] )¶
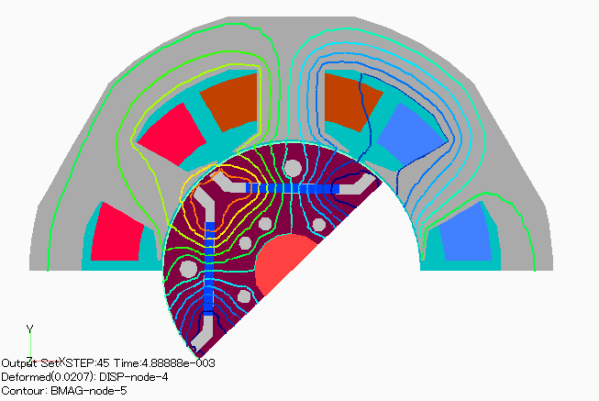
図 61 D1model 1Arms, 電流進角0deg (出典:[CITE2013] )¶
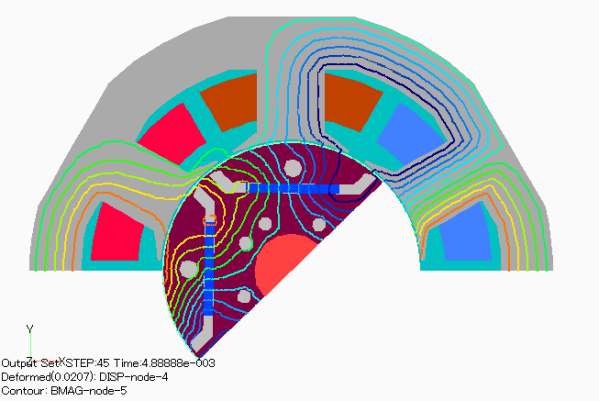
図 62 D1model 7.5Arms, 電流進角0deg (出典:[CITE2013] )¶