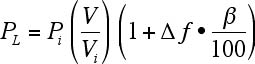付録1.　Y法モデルの概要⁽¹⁾

　標準系統モデルの検討に用いた「電力系統動特性解析プログラム（Y法）」のモデルの概要について以下に述べる。

　1. 発電機モデル

　発電機モデル（Parkモデル）の表現方法は，制動巻線回路の設定個数によって異なる。Y法では，制動巻線が全くない発電機から最大d軸1個，q軸2個までを持つ発電機を任意に選択できる。なお，利用の便のため，Xd' 背後電圧一定モデルを設定することもできるようにしている。この発電機形式は LGT で次のように指定できる。

　

LGT	モデルの種類
1	Xd' 背後電圧一定モデル
2	制動回路無しの発電機（小容量突極機）
3	q軸制動回路だけある発電機（インターポールダンパー付突極機）
4	d-q軸各1個の制動回路をもつ発電機（フルダンパ突極機と一般円筒機）
5	d軸1個，q軸2個の制動回路をもつ発電機（大型円筒機）

　また，発電機の空隙磁束飽和（無負荷飽和曲線に相当）は，円筒機，突極機ともd-q軸合成起磁力に対して適用する方法を用いている。中地域研究会および系統解析技術連絡会で収集された発電機定数データにもとづく標準定数より，標準系統モデルの中で利用した火力(NGT=2)，原子力(NGT=6)および水力発電機定数(NGT=8)を 付表1.1 に示す。

　標準系統モデルに使用した発電機モデルとしては，フルダンパ突極機と一般円筒機として最も一般的に用いられている上述したLGT=4を使用している。

　2. 励磁系モデル

　標準系統モデルに使用した以下の励磁系モデルを 付図1.1 に示す。

• 回転形励磁機用モデル（LAT=1）
• サイリスタ励磁機用モデル（LAT=2）
• ΔP形PSS付サイリスタ励磁機用モデル（LAT=102）（LAT=2のモデルにPSSを付加）

　界磁電圧EFは，無負荷，定格回転数，定格端子電圧時(EA=1.0 [pu])を1.0 [pu]とする値であり，有効電力Pの単位は発電機容量ベース（MVAベース）のpu値である。

　サイリスタ励磁機用モデルに付加しているΔP形PSSは，標準系統モデル中の発電機は縮約され大容量かつ長距離送電線に接続されることを考慮し，大容量原子力機(NGT=6)に発電機容量ベースで0.5 [pu]のリアクタンスのみを介して無限大母線に接続した場合を想定している。なるべく簡略化させるため，PSSの位相進み遅れ要素は1段のみとした。

　このPSS定数は比較的長距離送電線に接続される発電機用にローカル動揺から長周期動揺の広い範囲でダンピングを向上させるように設定した一例である。PSS定数は発電機励磁系定数，系統条件に大きく影響を受ける。特に，送電線が比較的短い場合，このPSSでは出力がリミッタにかかり動揺の減衰が悪くなるため，PSS回路の定常ゲイン(1.0)をより小さくする必要があるかもしれない。（定常ゲインの最大値は一般に，1.0以下）

　3. 調速機系モデル

　標準系統モデルに使用した以下の調速機系モデルを 付図1.2 に示す。

• 火力・原子力機用モデル（LPT=1）
• 水力機用モデル1（LPT=3）
• 水力機用モデル2（LPT=4）

　タービン出力の単位は発電機出力ベース（MWベース：定格MWを発生させるタービン出力を1 [pu]とする）である。

　ガバナ運転余裕は定格MW出力に対する割合[%]で設定する（Y法ではこの値をPLMと呼んでいる）。

(1) ガバナフリー(G.F.)運転（PLM≧0の場合)

　初期出力値（＝負荷設定値65M）に対して，定格MW×PLM÷100までガバナフリーによる出力増加が可能となる。

すなわち，

• 負荷設定(65M) = 初期出力値
• 負荷制限器(77M) = 65M + 定格MW出力×PLM [%]

となる（ 付図1.3 参照）

　ただし，PLM=0とした場合は上記77MがY法のガバナ標準ブロックのリミッター上限（UL）となる。

(2) ロードリミット(L.L.)運転（PLM＜0の場合)

　PLMを負で入力すると，

• 65M = 初期出力値 +（定格MW出力×PLM [%]の絶対値）
• 77M = 初期出力値

と設定され，ロードリミット運転となる（ 付図1.4 参照）。

　4. 負荷モデル

　負荷特性には静特性と動特性があり，それぞれに電圧特性，周波数特性などが考えられる。標準系統モデルでは，有効電力負荷PLが，負荷端電圧Vが 0.7 [pu] 以上の時，定電流特性（定I特性）で，0.7 [pu] 以下の時，定インピーダンス特性（定Z特性），無効電力負荷QLを定Z特性とするNLT=2という特性を標準とした（ 付図1.5 参照）。

【NLT=2の負荷特性】

負荷端電圧V≧0.7 [pu]の時，

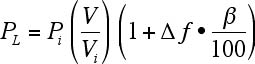　　　　（付1.1）

V＜0.7 [pu]の時，

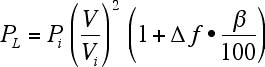　　　　（付1.2）　

Vの値に関わらず，

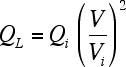　　　　　　（付1.3）

ただし，Pi, Qi：初期有効・無効電力負荷，Vi：初期電圧，β：周波数特性指数 [%／Hz]，Δf ：周波数偏差 [Hz]

　ただし，このNLT=2はV=0.7 [pu]でPLが不連続に変化するため，参考として，上記NLT=2の負荷特性の定I特性と定Z特性の切替を連続的に変化するようにしたNLT=107（ 付図1.6 参照）および全電圧領域で定Z特性とするNLT=0（または1）についても一部検討を行っている。

【NLT=107の負荷特性】

負荷端電圧V≧0.7 [pu]の時，

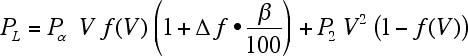　　　（付1.4）

V＜0.7 [pu]の時，

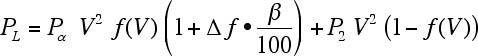　　　（付1.5）

Vの値に関わらず，

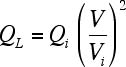　　　　（付1.6）

ここで，

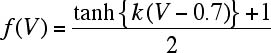　　　（付1.7）

また，Pα，P2は次式を満足するように求められる。

ただし，β：周波数特性指数 [%／Hz]，k：定数（=10.0），ΔL／Li：定数（=0.15）

【参考文献】

(1)「大規模電力系統の安定度総合解析システムの開発」，電力中央研究所　総合報告：T14，平成2年4月